立方型状态方程概述

         状态方程的开发经历了由最初的经验表达到具有一定理论基础的发展过程。理想气体状态方程是形式最简单的状态方程，但它不适用于真实气体。范德华方程是第一个适用于真实流体的状态方程，也是最早可用于气液两相计算的状态方程，其表达式为：z=V/(V-b)-a/(RTV)，这里的参数a、b分别反映了分子之间的吸引和排斥作用，它在一定程度上体现了真实流体分子间的相互作用，且三次多项式的特点也使得气液平衡的计算成为可能，它可定性的描述出高压下5种不同类型的相图。虽然范德华方程的计算精度并不高，但后来工业上广泛应用的立方型状态方程都是在范德华方程的基础上对引力项进行修正和改进得到的，例如，Redlich-Kwong (RK) 方程、Soave-Redlich-Kwong (SRK) 方程、Peng-Robinson (PR) 方程、Patel-Teja (PT) 方程等等。

1873年，范德华提出了最早可用于气液两相计算的状态方程，其表达式为：

                                         (1)

式中，z为压缩因子(z = pV/RT)，T为温度，V是体积，p是压力，R是气体普适性常数。参数a是分子间吸引力的度量，参数b是由于分子间斥力对分子体积的修正(如果分子为直径σ的硬球，则b=2πNσ³/3)，参数a、b可以由流体的临界性质计算得到。根据分子间排斥力和吸引力对状态方程贡献的不同，范德华方程也可以看作由硬球项(排斥项) + 吸引项所组成的方程。范德华方程只能对气、液相以及两相的相互转换进行定性的描述。对临界性质的计算以及对汽液平衡的计算误差则较大。如由范德华方程预测不同流体的临界压缩因子的值均为0.375，而实际流体的临界压缩因子在0.24到0.29之间。随后，范德华方程被许多计算精度更高的方程所取代，这些方程通常在范德华方程的基础上对其斥力项和/或引力项进行修正和改进得到的。

1949年，Redlich和Kwon对范德华方程的引力项进行了修改，提出了RK状态方程：

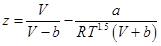                                (2)

对纯物质，RK方程参数a、b的表达式为：

              (3)

式中，R为气体普适性常数，T_C、p_C分别代表临界温度和临界压力。Carnahan和Starling用RK状态方程计算了各种纯物质的气相生成焓，其中包括一些极性以及/或者非对称物质，结果显示RK方程的计算精度较范德华方程有显著的提高。Abbott用RK方程计算了简单纯流体如Ar、Kr和Xe (它们的偏心因子都等于零)，得到较好的计算结果，但是对于偏心因子不等于零的复杂纯流体的计算结果并不理想。当结合一定的混合规则，RK状态方程就可以用于混合体系的计算了。Joffe和Zudkevitch用RK方程预测二元混合物的临界性质时发现计算结果可以通过调节参数a的值而得到大幅度的提升，Spear等人证实了RK方程可以计算二元混合物临界性质。Spear等进一步计算了三元混合物的性质，结果发现用RK状态方程计算三元混合物的精度比其构成的二元体系的计算精度稍差一点。RK状态方程虽然也仅有两个参数，但计算精度确比范德华方程有较大提高，尤其适用于非极性和弱极性的物质，不过对强极性的物质计算偏差仍然较大。另外，RK方程计算得到的临界压缩因子为0.333，比范德华方程的0.375更接近真实流体，说明RK方程在临界点附近的计算偏差仍然较大。

1972年，Soave提出用温度相关的a(T)来取代RK方程中的a/T^1.5，提出了SRK状态方程，即：

                                  (4)

式(4)中

          (5)

其中，ω是偏心因子。对一些烷烃化合物的蒸汽压和含烷烃二元体系的相行为研究发现，相对于RK方程，SRK方程能更好的拟合实验数据，而且能够预测二元体系在临界区的相行为。Elliott和Daubert用SRK状态方程关联了95种二元体系(其中包括烷烃、氢气、氮气、二氧化硫、一氧化碳和二氧化碳)的气液平衡，发现SRK方程可以提高这些混合物临界性质的计算精度，Han等也给出了对称体系以及含甲烷体系汽液平衡的计算结果。SRK状态方程的计算精度要比RK方程高，特别是应用于气液平衡的计算时，所得结果较为精确，但是，SRK方程计算得到的临界压缩因子与RK方程同样为0.333，并没有改进。

1976年，Peng和Robinson将SRK状态方程中的a(T)进行重新定义：

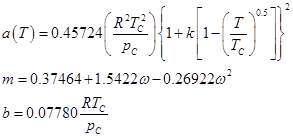      (6)

由于意识到RK和SRK状态方程的临界压缩因子的值0.333仍被高估了，于是提出了一种新的体积依赖关系式：

                     (7)

式(7)被称作PR状态方程，它将RK和SRK状态方程被高估的临界压缩因子进一步改进到0.307。用PR状态方程计算纯物质的饱和蒸汽压和摩尔体积，以及二元、三元甚至多元混合物的相行为发现，PR方程可以精确地预测纯物质的饱和蒸汽压和混合物的相平衡，计算结果至少和SRK方程相当，有的优于SRK方程。Han等也报道了PR状态方程在计算含氢气和氮气的混合体系的汽液平衡时更具优势。虽然PR方程仍是两参数状态方程，但由于PR方程较RK方程和SRK方程改变了体积（比容）函数，因而它对体积计算的精度较RK和SRK方程都有所提高。

    1976年，Fuller提出了一个三参数的状态方程：

                                      (8)

Fuller方程中参数c定义为协体积和体积的比例(β=b/V)，即：

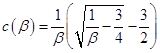                                     (9)

方程中的其他参数可由下面式子计算：

                            (10)

 临界压缩因子的表达式为：

                (11)

Fuller方程的修正包括两个特点：1）对于不同物质可得到可变的临界压缩因子，而不会像两参数方程那样，临界压缩因子的值为一定值；2）一个新的普遍化温度函数的产生使得方程中的参数a和b都变成了温度的函数。实际上，Fuller方程可以退化为SRK方程或者范德华方程。当β_C=0.259921，c=1，Ω_a=0.4274802，Ω_b=0.0866404，z_C=0.333，方程即退化为SRK状态方程；若β_C取1/3，c=0，Ω_a=0.421875，Ω_b=0.125，z_C=0.375，Fuller方程退化为范德华方程。Fuller状态方程关联饱和液体体积的均方根偏差在5%以内，且其对蒸汽压的计算精度也较SRK状态方程有所提高，计算结果显示Fuller方程甚至能够在合理的准确度下描述极性分子的相行为。

上述方程都是对范德华方程的引力项进行修正得到的，它们共同的特点是都可以展开成体积的三次方程，因此这类方程被统称为立方型状态方程。表1列出了其他一些对范德华方程引力项进行修正所得到的立方型状态方程和它们所对应的引力项表达式。立方型状态方程的求解可以使用解析法，但是工程上一般使用迭代法，这类方程计算耗时少，还可以进行手算，因此被广泛应用。对于三参数或者更多参数的立方型方程而言，最大的缺陷是额外参数的确立需要额外的纯物质数据。如将方程扩展到混合体系时，也至少要增加一个甚至更多的混合规则，且表达式也相对复杂，这不利于工业应用；而两参数的立方形状态方程，如SRK和PR方程，它们的表达形式简单，在工业应用时，仅需要知道物质的临界性质和偏心因子就可以方便的计算得到方程参数a、b，计算用时短且计算精度也满足工业需求，因此，SRK方程和PR方程在工业上应用最为广泛。

除了对范德华方程的引力项进行修正外，还有对范德华方程斥力项的改进（如表2所示）以及对引力项和斥力项同时进行修正。

 表1 对范德华方程引力项的改进

表2 对范德华方程斥力项的改进